GETEX (1999)
Deutsches Technologie-Experiment zur ETS-VII
Vom 19. bis 21. April 1999 wurde das Tele-Robotik- und Programmiersystem des DLR zur Steuerung des Roboterarms auf dem japanischen Satelliten ETS-VII eingesetzt. Die Hauptziele der deutschen ETS-VII Technologieexperimente (GETEX) waren die Verifizierung unserer tele-robotischen Bodenkontrollstation für die Fernsteuerung eines frei schwebenden Roboters, insbesondere die Durchführung eines Pflock-in-Loch-Experiments unter Verwendung von VR-Methoden und des "Vision&Force" Kontrollschemas, durch das Schließen von Sensorkontrollschleifen direkt an Bord (Kraft) und über die Bodenspur (Sicht), um so unsere sensorbasierten Autonomiefunktionen zu beweisen, Experimente durchzuführen, die für das Verhalten des ETS-VII im Freiflugmodus relevant sind, und so die bestehenden dynamischen 6-DoF-Modelle für die Interaktion zwischen einem Roboter und seinem frei fliegenden Trägersatelliten zu überprüfen.
Alle Experimente wurden live im Internet per Videoübertragung und einer VRML-Simulation gezeigt, die den aktuellen Status von Roboter und Satellit auf beeindruckende Weise darstellte.
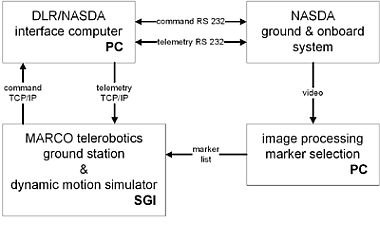
Um unsere Schnittstellen sowie unser MARCO-Steuerungssystem im Rahmen des ETS-VII-Szenarios zu überprüfen und zu testen, wurde ein Online-Simulator entwickelt, der den ferngesteuerten Roboter, seine Befehlsschnittstellen und seine Umgebung emuliert. Der Simulator ist in der Lage, alle verschiedenen Modi, das Timing, die Interaktionen mit der Umgebung und die Vorhersage der Lage des Satelliten bei der Bewegung des Roboterarms zu emulieren. Diese Art der Simulation hat sich als sehr nützlich erwiesen, um die Korrektheit der Software bei der Interaktion mit dem Tele-Roboter zu überprüfen.
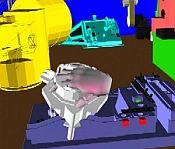
Peg-in-Hole-Experiment mit VR-Methoden und dem "Vision&Force"-Kontrollschema
Nach dem Anlernen der gewünschten Peg-in-Hole-Aufgabe in der VR-Umgebung, d.h. der Auswahl von TBTL (TaskBoard TooL) und der Platzierung in HOLE A, wurde die Ausführung gestartet und vollautomatisch an Bord durchgeführt:

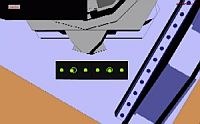
Um die TBTL zu erhalten, führten wir zunächst eine visuelle Servo-Aufgabe durch, bei der einige Marker-Merkmale im Videobild verwendet wurden, um den Werkzeugmittelpunkt (TCP) des Roboters autonom in die gewünschte sensorbezogene Pose zu steuern. Zu diesem Zweck haben wir einen Ansatz entwickelt, der keine Kalibrierung benötigt. Das Kontrollgesetz kann wie folgt geschrieben werden
vc = a C (s-s*)
wobei (s-s*) die vektorwertige Abweichung zwischen dem aktuellen und dem nominalen Sensormuster ist, die die Verschiebung der aktuellen Roboterpose x von der nominalen Pose x* angibt. vc ist der Geschwindigkeitsbefehl, a steht für einen skalaren dynamischen Ausdruck, mindestens eine reelle Konstante, der das Verhalten des geschlossenen Regelkreises bestimmt, und C steht für einen Projektionsoperator, der für die Abbildung des Sensorraums in den (kartesischen) Kontrollraum verwendet wird. C wird durch das Lernen eines neuronalen Netzwerks oder durch analytische Methoden bestimmt
Wir haben die analytische Methode zur Bestimmung von C angewandt, die durch die Pseudoinverse der Jacobi-Matrix der m Abweichungen im Sensorraum im Verhältnis zu den n Abweichungen im Kontrollraum dargestellt wird. Dazu haben wir den TCP des Roboters in allen n=6 Freiheitsgraden ein wenig hin und her bewegt, die entsprechenden Sensorwerte aufgezeichnet und die Jacobimatrix aus den resultierenden Differenzquotienten gebildet.

Wir haben die experimentelle Bestimmung von C sowohl in unserer Simulationsumgebung als auch in der realen Umgebung durchgeführt. Das Ergebnis war nahezu identisch, was auf die Genauigkeit unserer Kamerasimulation zurückzuführen ist. Die Kameraparameter wurden mit einem selbst entwickelten Tool zur Kamerakalibrierung geschätzt.
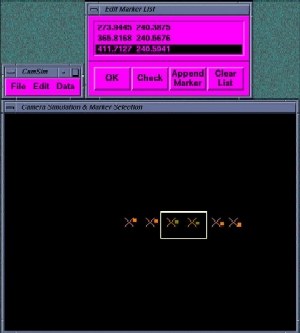
Für die Steuerung verwendeten wir die TaskBoard-Marker-Funktionen, die ursprünglich zur Verfügung standen, um den TCP in die richtige Position zu tele-operieren. Ziel war es, die Marker im Live-Videobild zu finden und den entsprechenden Befehl für den geraden Weg zu erzeugen, um den Roboter in die gewünschte (sensordefinierte) Zielposition zu bringen. Um den bildverarbeitungsbasierten Sensorregelkreis zu überprüfen, wurde der TCP absichtlich in eine Position bewegt, die von der optimalen Zielposition abwich (einige Zentimeter in allen Translationsrichtungen und etwa 20 Grad in der Z-Rotation).
Nach 3 Zyklen (mit a = 1) war die Zielposition erreicht. Um die Marker aus dem Videobild zu extrahieren, wurde ein Blob-Finding-Algorithmus verwendet. Da dieser Algorithmus mehr "Marker" als gewünscht lieferte, z.B. aufgrund schlechter Beleuchtungsbedingungen, wurden die Marker interaktiv ausgewählt und der daraus resultierende Steuerbefehl wurde verifiziert, bevor er an den realen Roboter gesendet wurde. Die Abbildung oben zeigt die simulierten (_) und die realen (X) Marker mit dem interaktiven Auswahlrahmen.
Die Unterschiede zwischen den Markierungen _ und X resultieren aus einer unterschiedlichen TCP-Position, um die beiden Darstellungen zu zeigen. Wenn sich der reale und der simulierte TCP in der gleichen Pose befinden, haben die realen und die simulierten Marker nahezu die gleichen 2D-Koordinaten.
Die simulierten und gemessenen Pixelkoordinaten sind in der Tabelle unten aufgeführt. Sie unterscheiden sich nur im Subpixelbereich.
X1 | Y1 | X3 | Y3 | X4 | Y4 | |
|---|---|---|---|---|---|---|
real | 273.8 | 240.1 | 365.7 | 240.3 | 411.6 | 240.3 |
0 | 7 | 0 | 5 | 0 | 7 | |
sim | 273.9 | 240.3 | 365.8 | 240.5 | 411.7 | 240.5 |
4 | 8 | 1 | 6 | 1 | 9 |
Tabelle 1 - gemessene und simulierte Pixelkoordinate
Dynamische Bewegungsexperimente
Ein großer Teil der GETEX-Experimentierzeit wurde für die so genannten "Dynamic Motion Experiments" verwendet, die aus einer Reihe von Manövern bestehen, die der Manipulator bei ausgeschaltetem Lageregelungssystem der ETS-VII durchführt.
Bei Weltraumrobotersystemen, die weder positions- noch lagekontrolliert sind, führt der Drehimpulserhaltungssatz zu einer Drehung des Raumfahrzeugs um einen Betrag, der sich aus den Massen- und Trägheitseigenschaften der Manipulatorglieder und des Raumfahrzeugs ergibt. Im Allgemeinen wird davon ausgegangen, dass auf solche frei schwebenden Roboter keine äußeren Kräfte einwirken.
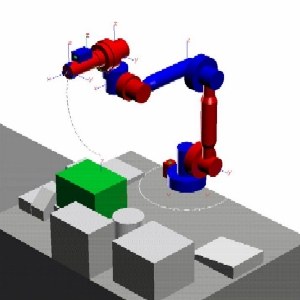
Solange die mit dem Roboter ausgeführten Aufgaben in roboterfixierten Koordinaten beschrieben werden, hat die Tatsache, dass die Position des Satelliten unkontrolliert bleibt, keinen Einfluss. Wird die Aufgabe jedoch in Bezug auf ein bahnfestes Koordinatensystem beschrieben, wie es zum Beispiel beim Einfangen eines anderen defekten Satelliten der Fall wäre, muss die Satellitenbewegung des Roboters berücksichtigt werden (siehe Abbildungen). Die Gleichungen, die die TCP-Bewegung mit der Bewegung der Manipulatorgelenke in Beziehung setzen und die bei Robotern mit einer trägen Basis rein kinematische Gleichungen sind, werden im Fall von frei schwebenden Raumrobotern von dynamischen Parametern abhängig, da die Impulsgleichungen zur Beschreibung der Satellitenbewegung verwendet werden.
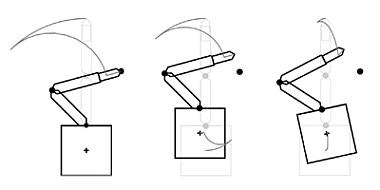
Dies beeinflusst die Methoden der Bahnplanung, die angewendet werden müssen. Einerseits sind Singularitäten, d.h. Gelenkkonfigurationen, in denen der Roboter in kartesischen Koordinaten nicht steuerbar ist, nicht mehr nur eine Funktion der Roboterkinematik, sondern werden auch von den dynamischen Eigenschaften des Roboters abhängig. Daher müssen iterative Methoden, die auf den direkten kinematischen Gleichungen basieren, anstelle der inversen kinematischen Gleichungen verwendet werden. Außerdem macht die Drehimpulsgleichung das System nicht-holonomisch, d.h. die Ausrichtung des Satelliten ist nicht nur eine Funktion der aktuellen Gelenkkonfiguration, sondern auch eine Funktion des gewählten Pfades.
Zwei unterschiedliche Pfade, die von der gleichen Ausgangskonfiguration des Roboters ausgehen und zur gleichen Endkonfiguration führen, führen daher zu unterschiedlichen Beträgen der Satellitendrehung - und damit auch zu unterschiedlichen endgültigen Trägheits-TCP-Positionen. Folglich bietet die Nicht-Holonomie die Möglichkeit, eine Neuausrichtung des Satelliten nur mit Hilfe der Bewegung des Manipulators vorzunehmen, indem einfach ein geschlossenes Manöver im Gelenkraum durchgeführt wird.
Unabhängig davon, welche Bahnplanungsmethode bei frei schwebenden Robotern angewendet wird, ist sie notwendigerweise stark modellbasiert. Die Parameter des dynamischen Modells müssen daher recht gut bekannt sein. Während dies für die geometrischen Parameter sowie für die Masse und Trägheit des Manipulators kein Problem darstellt, unterliegen die Masse und die Trägheit des Raumfahrzeugs während der Lebensdauer eines Wartungssatelliten erheblichen Veränderungen. Dies ist insbesondere dann der Fall, wenn das Raumfahrzeug Einfang- oder Rendezvous-/Docking-ähnliche Operationen durchführt.
Ein Ziel der GETEX-Experimente war es daher, die Masseeigenschaften des Satelliten nach eineinhalb Jahren Aktivität in der Umlaufbahn zu ermitteln. Weitere Ziele waren die Überprüfung der dynamischen Modelle und die Gewinnung von Erkenntnissen über die Art und Bedeutung der Störungen, die auf einen Robotersatelliten in einer niedrigen Erdumlaufbahn einwirken. Außerdem sollten Daten für die zukünftige Entwicklung von Steuerungen gesammelt werden, die die Bewegungssteuerung des Manipulators mit der Lageregelung des Satelliten kombinieren. Um all diese Ziele zu erreichen, wurde eine Vielzahl verschiedener Manöver vom Manipulator ausgeführt, während das Lageregelungssystem von ETS-VII ausgeschaltet war.
Experimente
Die folgenden Manöver des Manipulators an Bord des ETS-VII Satelliten wurden durchgeführt:
- Punkt-zu-Punkt-Manöver
- Manöver zur Bestimmung einer Variation der Lage des Satelliten
- optimierte Manöver zur Minimierung der Bewegung der Satellitenbasis oder der Manipulator-Gelenkbewegung (Minimalenergie-Manöver)
Während der ersten Hälfte der Experimente wurde das Lageregelungssystem des Satelliten in den "frei schwebenden Modus" geschaltet, der einen frei schwebenden Zustand des Systems innerhalb eines Lagebereichs von wenigen Grad ermöglicht. Da der Satellit im normalen Betriebsmodus eine nominale Winkelgeschwindigkeit hatte, die der Umlaufgeschwindigkeit entsprach, so dass er immer in die gleiche Richtung zur Erde zeigte, blieb die Winkelgeschwindigkeit des Satelliten auch während der Experimente mit der frei schwebenden Bewegung unverändert, da der Satellit aufgrund seiner Trägheit weiter rotierte.
Die Experimente wurden in fünf Zeitabschnitten von je zwanzig Minuten durchgeführt, wobei die ersten zehn Minuten im frei schwebenden Modus und die letzten zehn Minuten mit eingeschaltetem Lageregelungssystem (AOCS) stattfanden.
In jedem Slot wurde die folgende Prozedur durchgeführt:
- Entladen der Impulsräder mit Hilfe der Lageregelungstriebwerke
- Reduzieren der Restwinkelgeschwindigkeit des Satelliten auf einen niedrigeren Wert durch erneutes Drehen der Impulsräder
- AOCS schaltete in den Freiflugmodus
- Manöver durchführen
- AOCS schaltete in den Impulsrad-Bewegungskontrollmodus
- Manöver wiederholen.
Ergebnisse der Experimente
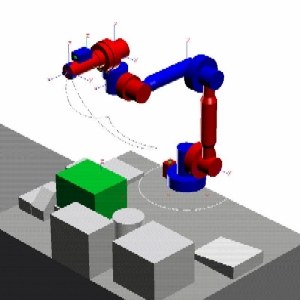
Die folgende Diskussion bezieht sich auf den ersten repräsentativen Slot von Experimenten, bei denen die in Abbildung 6 gezeigten Manöver nacheinander durchgeführt wurden. Die Abbildung zeigt die Bewegung des Endeffektors (durchgezogene Linie), die mit einem idealen frei schwebenden Modell (frei von äußeren Einflüssen) simuliert wurde. Beachten Sie, dass das erste Manöver ein Punkt-zu-Punkt-Manöver ist, während das zweite ein Manöver mit geschlossenem Regelkreis ist.
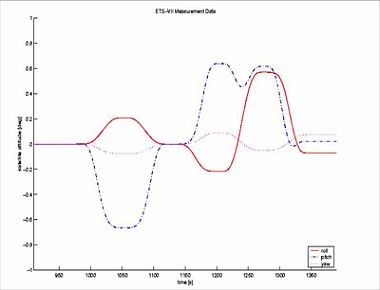
Es wurde festgestellt, dass die reale Bewegung des Endeffektors in Bezug auf den Satelliten mit der simulierten Bewegung übereinstimmt. Es wurde festgestellt, dass die Bewegung der Satellitenlage während des frei schwebenden Zustands von der simulierten Bewegung abweicht, wie in den Abbildungen 7a und b dargestellt. Die Abbildungen zeigen die Euler-Parameter, die die Satellitenlage relativ zum Orbitalrahmen in Abhängigkeit von der Zeit beschreiben.
Von Interesse ist auch der Drehimpuls der Reaktionsräder, der in Abbildung 8 für die gesamte Dauer des ersten Slots dargestellt ist. Die Abbildung zeigt, dass der Drehimpuls während der Zeit des freien Schwebezustands des Experiments (910-1360 Sekunden) aufgrund der zweiten Phase in der oben erwähnten Sequenz einen kleinen Wert ungleich Null hatte.
Analyse der Ergebnisse
Abbildung 7a zeigt, wie der Vergleich der Anfangs- und Endwerte der Fluglageparameter zeigt, dass das Manöver im geschlossenen Regelkreis zu einer kleinen Variation der Satellitenfluglage führt.
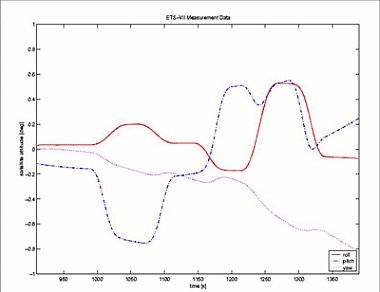
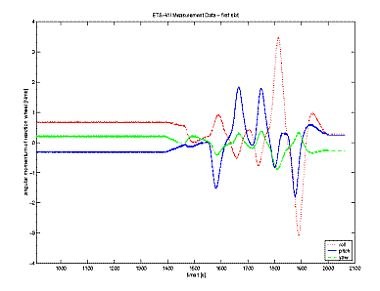
Abbildung 7b zeigt jedoch eine beträchtliche Drift des Satelliten, die die Bewegung überlagert, die durch die Bewegung des Manipulators in Abbildung 7a verursacht wird. Es hat sich gezeigt, dass diese Drift hauptsächlich von den folgenden Faktoren abhängt:
- dem Schwerkraftgradienten, der auf den Satelliten einwirkt
- der Kopplung zwischen dem Restdrehimpuls der Impulsräder und
- der orbitalen Winkelgeschwindigkeit des Satelliten der Restwinkelgeschwindigkeit des Satelliten in Bezug auf den orbitalen Bezugsrahmen zu Beginn des Experiments.
Andere Faktoren, wie die Wechselwirkung des magnetischen Dipols des Satelliten mit dem Magnetfeld der Erde, der Sonnendruck und der Luftwiderstand wurden als Effekte zweiter Ordnung betrachtet. Der Luftwiderstand wurde in der Tat von der NASDA gemessen und erwies sich als geringfügig. Schließlich wurde festgestellt, dass bewegliche Teile des Satelliten, wie die Solarpaneele und die Kommunikationsantenne, nach der Simulation eine kleine Störung der Bewegung des Satelliten um die Nickachse verursachen.
Die simulierten Daten des aktualisierten Mehrkörpermodells, das die oben genannten Punkte berücksichtigt, sind in Abbildung 9 (gepunktete Linien) im Vergleich zu den gemessenen Daten (durchgehende Linien) dargestellt. Aus dieser Abbildung ist ersichtlich, dass es immer noch eine Diskrepanz zwischen den beiden Datensätzen gibt. Man nimmt an, dass dies auf einen Näherungswert für die Masse und die Trägheit des simulierten Modells im Vergleich zur Realität zurückzuführen ist, da sich die Ergebnisse als sehr empfindlich gegenüber Schwankungen der simulierten Werte erwiesen. Denn obwohl die Eigenschaften des Manipulatorarms durch Messungen vor dem Start bekannt sind, sind die des Satelliten aufgrund des Treibstoffverbrauchs während der Lebensdauer des Satelliten nur ungefähr bekannt. Eine Schätzung der anfänglichen Trägheit des Satelliten war ebenfalls notwendig, da die Masse- und Trägheitsdaten nur beim Start für das komplette System mit dem Manipulator in der verstauten Konfiguration bekannt waren.
Es kann ein Parameteridentifikationsproblem definiert und gelöst werden, so dass diese Größen bestimmt werden können. Beachten Sie, dass die unbekannten Größen die Masse und Trägheit des Satelliten und die Position des Massenschwerpunkts des Mehrkörpersystems sind. Wenn dieses Problem gelöst wird, kann eine neue Methode zur Messung der Masse- und Trägheitseigenschaften eines Weltraumroboters in der Umlaufbahn entwickelt werden.

Die experimentellen Ergebnisse haben auch gezeigt, dass die Modellierung des externen Drehmoments, das auf den Satelliten einwirkt (Standardstörungen, die auf Raumfahrtsysteme in der Umlaufbahn einwirken), in das Gesamtmodell des Systems einbezogen werden muss, wenn die Manöver des Manipulators auf den Inertialraum oder auf ein anderes Raumfahrzeug bezogen werden müssen. Bei der Entwicklung des für dieses Experiment verwendeten Modells wurde davon ausgegangen, dass solche Störungen für die Zwecke des Experiments vernachlässigbar sind. Der Grund dafür ist, dass die Dauer der Manöver als kurz genug angesehen wurde, um jegliche externe Einwirkung auf den Satelliten zu vernachlässigen.
Die unerwartete Drift des Satelliten in der Zeit führte zu einem teilweisen Scheitern des zweiten oben aufgeführten Manövers, da es nicht möglich war, die Rotation des Satelliten in Bezug auf den Inertialraum während des Experiments zu bestimmen. Trotz dieses unerwarteten Verhaltens des Systems konnten jedoch alle Manöver durchgeführt werden, wobei die Beschränkungen für die Variationen der Satellitenlage von 1 Grad um jede Achse in einem akzeptablen Maß eingehalten wurden.
Zusammenfassend lässt sich sagen, dass das GETEX-Experiment zur dynamischen Bewegung nützlich war, um das Modell des ETS-VII-Satellitenmanipulatorsystems für Manöver zu validieren, die sich auf den Satellitenrahmen beziehen, und um zu erkennen, dass es für eine korrekte Modellierung der Manöver, die sich auf den festen Inertialrahmen beziehen, notwendig ist, die externen Störungen zu berücksichtigen, die auf ein Raumfahrzeug in einer niedrigen Erdumlaufbahn einwirken, und um ein Modell für die externen Störungen zu entwickeln, das mit den experimentellen Daten validiert werden kann.
