Synchronisierung und Kalibrierung

Das beim DLR Multisensory 3D-Modeler realisierte Konzept der multisensoriellen Datenerfassung in Echtzeit erfordert nicht nur eine zeitliche Synchronisation, sondern auch eine räumliche Kalibrierung, um die 3D-Sensordaten im selben Weltkoordinatenrahmen verorten zu können.
Konzept für die Synchronisation von Hard- und Software
Der DLR Laser Range Scanner ist die zentrale Komponente dieses Konzepts. Seine Anbindung erfolgt über den CAN-Bus (CAN: Controller Area Network), einem echtzeitfähigen Feldbus mit Priorisierung. Die Zusammenführung mehrerer Sensoren mit verschiedenen Schnittstellen stellt in der Sensorsynchronisation ein großes Problem dar. Dieses Problem wird durch die Nutzung eines CAN-Busses als Master-Synchronisationsbus für Zeitstempel behoben. Jeder Sensor empfängt denselben Videosynchronisationsimpuls (erzeugt zum Beispiel durch die Videokameras), was in synchronen Messungen resultiert. Der Laser Range Scanner erzeugt sein internes Taktsignal aus dieser Quelle. Da der Abtastkopf mit 25 Umdrehungen pro Sekunde rotiert, wird alle 40 ms eine neue Zeitstempelnachricht auf dem CAN-Bus gesendet. Diese Nachrichten werden von allen Sensoren empfangen, die dadurch wiederum veranlasst werden, ihre Datensätze entsprechend zu übertragen. Zusätzlich zum Laser Range Scanner sendet der Posesensor (Position und Orientierung) seine Daten direkt über den CAN-Bus. Jeder an den CAN-Bus angebundene Sensor kann somit die Pose seines lokalen 2D-Datensatzes zum globalen Rahmen in Bezug setzen.
Jede Nachricht auf dem CAN-Bus wird gemäß ihrer Priorität verarbeitet. Hohe Priorität haben zum Beispiel Nachrichten, die Befehle und Synchronisationsinformationen enthalten, weil deren Übermittlung bzw. Verteilung zeitkritisch ist. Die Synchronisationssignale haben eine niedrigere Priorität als Befehle, aber eine höhere als die Abtastdaten des Laser Range Scanners. Die Posedatensignale weisen die niedrigste Priorität auf, weil aufgrund des Zeitstempels eine Verzögerung dieses Signals im Verhältnis zur entsprechenden Daten- und Synchronisationsnachricht keine Falschzuordnung zulässt und die Zusammenführung so auch im Anschluss erfolgen kann. Die Baudrate auf dem CAN-Bus beträgt 1 Mbit/s. Die 2,5D-Datensätze des Streifenlasersensors und die Bilddaten der Textursensoren werden über die zeitliche Zuordnung mithilfe des Zeitstempels mit den Lagedaten zusammengeführt. Anwendungen können auf die Daten über ein vereinheitlichtes RPC-Protokoll (Remote Procedure Call) zugreifen, das auf TCP/IP aufsetzt. Diese Schnittstelle ist dieselbe wie für die Daten des Laser Range Scanners (die Anwendungsschicht kann auf den CAN-Bus nicht zugreifen und wird als internes Bussystem behandelt).
Alle Sensoren sollten synchron messen können, um die Prinzipien der Datenfusion realisieren zu können. Aus diesem Grund sollten sich die Sensoren nicht gegenseitig stören oder beeinträchtigen. So sollte der Laserstrich des Laser Range Scanners zum Beispiel nicht auf den Bildern des Textursensors zu sehen sein, wenn sie gleichzeitig genutzt werden. Eine mögliche Lösung ist die phasenverschobene Abtastung von Laser Range Scanner und Textursensor – die Kamera macht Aufnahmen, wenn der Laser nicht sichtbar ist. Es besteht die Möglichkeit, beim Abtasten der Objektoberfläche mit dem Laser Range Scanner automatisch Informationen über deren Textur zu gewinnen. Der Laser Range Scanner sollte nicht durch den Laserstreifensensor gestört werden. Dies wird durch die Umfeldhelligkeitskompensation des Laser Range Scanners verhindert. Die IR-Blitzlichter des Trackingsystems verursachen Störungen bzw. Rauschen bei den Messungen des Laser Range Scanners. Da die zeitliche Beziehung zwischen Videoimpuls und Auftreten des Blitzes bekannt ist, können wir die innerhalb der Blitzperiode gemessenen Werte ausschließen.

Räumliche Sensorkalibrierung
Die Transformation der Daten xsensor im Sensorkoordinatensystem CoSsensor auf das Koordinatensystem des Positionssensors des Tool Center Points (TCP, Hauptbezugspunkt des Effektors bzw. Sensors) CoStcp wird beschrieben durch die Rotationsmatrix Rsensor mit anschließender Translation Tsensor. CoSbase beschreibt den globalen Koordinatenrahmen des Lagesensors (siehe Abb. 2). Der Lagesensor misst einen sechsdimensionalen Vektor, der sich aus drei translatorischen und drei rotatorischen Parametern zusammensetzt. Die Transformation von CoSsensor zu CoStcp ist für jede Sensorart anders. Sie hängt von der Anbringung des jeweiligen Sensors im handgeführten Gerät ab. In der Regel sind die Parameter der Matrix Rsensor und Tsensor anfangs unbekannt. Bei der Sensorkalibrierung geht es um die Identifizierung dieser sechs Parameter.
Kamerakalibrierung und -entzerrung
Im Rahmen der Kamerakalibrierung werden alle intrinsischen und extrinsischen Parameter für die Beschreibung des Projektionsverhaltens der Kamera durch ein mathematisches Modell bestimmt. Viele Kameras lassen sich als Lochkameras mit zwei radialen Verzeichnungskoeffizienten beschreiben. Daraus ergeben sich 7 intrinsische Parameter. Des Weiteren wird die Transformation zwischen Kamera und einem Weltkoordinatensystem mithilfe von sechs extrinsischen Parametern (d. h. Translation und Rotation) modelliert.
Entzerrung
Die Verzerrung bzw. Verzeichnung der Bilder durch die Kameraobjektive muss im Hinblick auf eine korrekte 3D-Rekonstruktion kompensiert werden. Wir verwenden dazu neben einem polynomialen Verzerrungsmodell dritter Ordnung auch ein radiales Verzerrungsmodell. Etwas bessere Ergebnisse konnten mit der polynomialen Verzerrung bei höherem Kalibrierungsaufwand erzielt werden.



Stereoalgorithmen brauchen nicht nur bekannte intrinsische Parameter (z. B. Verzerrung), sondern auch bekannte externe Kalibrierungsparameter (Geometrie zwischen den Stereokameras), um Stereokorrespondenzen einfach entlang von (Epipolar-)Linien finden und die Geometrie des gemessenen Objektes genau rekonstruieren zu können.
Die obigen Abbildungen zeigen die verzerrten Originalbilder neben dem korrigierten Stereobild.
Einzelkamerakalibrierung
Die Kalibrierung erfolgt durch die Aufnahme von Bildern eines Objekts, dessen Maße genau bekannt sind (d. h. Kalibrierobjekt). Ein flaches Kalibriergitter lässt sich einfach und genau mit einem herkömmlichen Drucker erstellen.
Die Einzelkamerakalibrierung umfasst folgende Schritte:
Mehrere Aufnahmen des Kalibriergitters aus verschiedenen Perspektiven machen.
- Automatische Detektion aller Kalibrierpunkte (d. h. Eckpunkte der Quadrate) im Bild.
- Berechnung aller Parameter aus bekannten Koordinaten aller Kalibrierpunkte in einem Weltkoordinatensystem und der jeweiligen Projektionen dieser Punkte in mehreren Bildern aus verschiedenen Perspektiven. Für die Berechnung wird der Algorithmus von Zhang, Sturm und Maybank verwendet.
Daraus ergeben sich sieben intrinsische und sechs extrinsische Parameter für jede Perspektive. Stereokameras werden kalibriert, indem beide Kameras gleichzeitig Aufnahmen des Kalibriergitters machen. Für jede Perspektive beschreiben die extrinsischen Parameter die Transformation in ein gemeinsames Weltkoordinatensystem. Die Transformation zwischen beiden Kameras wird erstmal nicht als konstant festgelegt. Daher gibt es bei der relativen Transformation für jede Perspektive leichte Abweichungen. Dies wird bei der Stereokamerakalibrierung berücksichtigt.
Stereokamerakalibrierung
Die Stereokamerakalibrierung wird folgendermaßen durchgeführt:
- Verwendung der Ergebnisse der Einzelkamerakalibrierung und erste Schätzung der relativen Transformation zwischen beiden Kameras aus der ersten Perspektive.
- Nicht-lineare Optimierung über alle Parameter hinweg durch Konstanthaltung der relativen Transformation zwischen den Kameras und Minimierung des Rückprojektionsfehlers bei allen Kalibrierpunkten.
Daraus ergeben sich 20 Parameter für das Stereokamerasystem, d. h. sieben intrinsische Parameter für jede der beiden Kameras und sechs Parameter für die relative Transformation zwischen beiden Kameras. Zusätzlich gibt es für jede Perspektive sechs Parameter für die Transformation von der Welt zur Stereokamera.
TCP-Kalibrierung
Diese Transformationen zwischen Weltkoordinatensystem und der Stereokamera für jede Perspektive sind normalerweise nicht erforderlich. Stattdessen ist im Bereich der Robotik eher die konstante Transformation zwischen den Kameras und dem Hauptbezugspunkt (Tool Center Point, TCP) von größerer Bedeutung.
Die TCP-Kalibrierung wird folgendermaßen durchgeführt:
- Mithilfe der Sensoren des Roboters, an dem die Stereokamera befestigt ist, die Transformation zwischen Basispunkt und TCP für jede Kalibrierperspektive aufzeichnen.
- Berechnen einer ersten Schätzung der konstanten Transformationen zwischen Weltkoordinatensystem und dem Basispunkt sowie zwischen TCP und den Stereokameras aus mehreren entsprechenden Basis-zu-TCP- und Welt-zu-Stereokamera-Transformationen z. B. unter Verwendung der Singulärwertzerlegung (SVD).
- Nicht-lineare Optimierung von beiden konstanten Transformationen durch Minimierung des Rückprojektionsfehlers bei allen Kalibrierpunkten.
Daraus ergeben sich 26 Parameter, die das Stereokamerasystem und die Transformation zwischen Stereokamera und TCP beschreiben.
Realisierung
Alle Schritte werden in einer anwenderfreundlichen Java-/C-Implementierung automatisch ausgeführt.
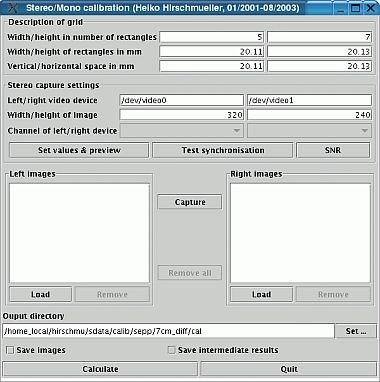
Zu den zukünftigen Aufgaben gehören die verbesserte Handhabung des Werkzeugs sowie die gesteigerte Robustheit der automatischen Kalibriergittererkennung.
Kalibrierung des DLR Laser Range Scanners
Für die Kalibrierung des Laser Range Scanners am TCP müssen wir lediglich diejenigen Parameter bestimmen, die die Transformation von CoSsensor zu CoStcp beschreiben, weil weder Verzeichnung noch Maßstab berücksichtigt werden müssen. Wir möchten Datenpunkte auf der Oberfläche einer Kugel mit gegebenem Radius bei beliebigem Mittelpunkt mit dem Laser Range Scanner gleichzeitig messen, wobei die TCP-Pose vom Posesensor geliefert wird. Für diesen Rechenschritt stützen wir uns auf das Levenberg-Marquardt-Verfahren, einem weit verbreiteten Optimierungsverfahren zur Lösung nichtlinearer Ausgleichs-Probleme mithilfe der Methode der kleinsten Quadrate. Es ist eine Kombination aus der Inverse-Hesse-Matrix-Methode und der Methode des steilsten Abstiegs. Es muss eine Bewertungsfunktion aufgestellt werden. Über deren Minimierung erhalten wir die am besten entsprechenden Parameter für unser Problem der Berechnung der konstanten Transformation zwischen Sensor und TCP.

Der Levenberg-Marquardt-Algorithmus erfordert für jede einzelne Messung ein Qualitätsmaß, z. B. Abweichung. Da der Algorithmus gegenüber Ausreißern sehr anfällig ist, die bei größeren Entfernungen zunehmen, nehmen wir die zunehmende Varianz bei größeren Abtastentfernungen, genähert über Exponentialfunktion, als Qualitätsmaß, sodass Messungen aus größerer Entfernung zu einem geringeren Grad berücksichtigt werden.
References
T. Bodenmüller, W. Sepp, M. Suppa, and G. Hirzinger. Tackling Multi-sensory 3D Data Acquisition and Fusion. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2007), pp. 2180-2185, San Diego, CA, USA, 2007.
M. Suppa and G. Hirzinger. A Novel System Approach to Multisensory Data Acquisition. Intelligent Autonomous Systems 8 (IAS-8), pp. 996-1004, Amsterdam, March 10-13, 2004.
