Dieses rasante exponentielle Wachstum trifft man in vielen Bereichen an. Nehmen wir mal Bakterien. Sie vermehren sich durch Zellteilung. Aus einem Bakterium werden zwei. Diese teilen sich nach dem Wachstum wieder, verdoppeln sich also jedes Mal. Wie viele Bakterien nach dem 5. Teilungsschritt entstanden sind, siehst du hier:
Aus jedem Bakterium entsteht (in unserem Beispiel innerhalb von 20 Minuten) ein weiteres. Man sagt dann, die „Reproduktionszahl“ (R) ist 1. Das führt schon nach kurzer Zeit zu einer unvorstellbar großen Anzahl. Im Grunde ist das genauso wie bei unserer Geschichte mit dem Taschengeld. Und auch bei der Corona-Pandemie – die nicht durch Bakterien, sondern durch Viren verursacht wurde – kann sich das so ähnlich entwickeln. Dabei geht es um die Frage, wie die Anzahl der infizierten Personen zunimmt.
Um zu besser zu verstehen, wie schnell sich eine Pandemie ausbreiten kann, wenn man nichts dagegen tut, haben wir hier eine Grafik erstellt. Sie zeigt die Entwicklung über einen Zeitraum von sechs Tagen. Dabei nehmen wir mal Folgendes an: Ein Mensch, der sich angesteckt hat, würde jeden Tag drei weitere Menschen anstecken (R = 3). Und wir nehmen auch an, dass alle Infizierten in diesen sechs Tagen weiter ansteckend bleiben. Was dann passieren würde, siehst du hier:
Verlauf innerhalb von sechs Tagen
Die einzelnen Bilder in dieser Grafik zeigen den Verlauf innerhalb von sechs Tagen – also von Montag bis Samstag. Auf jedem Bild sind für jeden Tag 1.024 Punkte (Personen) angeordnet. Nicht-infizierte Personen sind graue Punkte, Infizierte sind rot, neu Infizierte orange dargestellt. Es geht bei diesem Bild nur um die Anzahl, der Abstand der Punkte ist unwichtig.
Stell dir vor, du würdest für jeden Tag die orangefarbenen und die roten Punkte übereinanderstapeln, wie die Euromünzen bei unserem Beispiel weiter oben. Wenn wir dann die Gipfel dieser „Türmchen“ verbinden, erhalten wir diese Darstellung.
Kurvenverlauf
Diese Grafik zeigt den Verlauf als Kurve. Sie beginnt ganz flach, steigt dann aber immer steiler an.
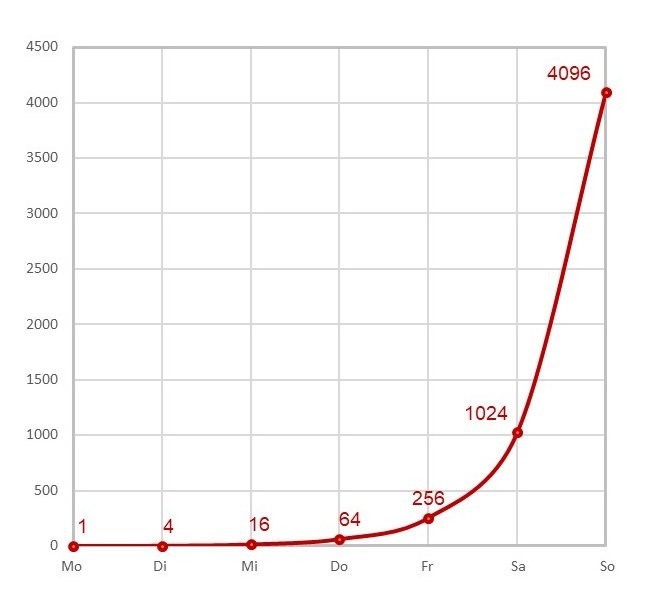
Man kann daraus ablesen, wie viele Infizierte es an einem Tag gibt: Nach sechs Tagen wären es 4.096 Infizierte. Ähnliche Infektionskurven kann man im Internet finden. Zunächst nimmt die Anzahl der Infizierten kaum merklich zu, aber dann geht es geradezu explosionsartig weiter. Die Kurve wird immer steiler und steiler: Jeden Tag werden immer mehr und mehr Personen infiziert.
In unserem Beispiel haben wir angenommen, dass die Reproduktionszahl 3 ist und dass jemand mindestens sechs Tage lang ansteckend ist. Das muss – je nachdem, um welche Krankheit es geht – nicht so sein. Wie groß die Reproduktionszahl einer Pandemie ist, hängt aber nicht nur von der Art der Krankheit ab, sondern auch von einigen anderen Bedingungen:
Wie lange dauert es, bis ein Infizierter wieder gesund ist bzw. wie lange kann er nach der Ansteckung selbst die Krankheit weitergeben?
Wie viele Personen in der Bevölkerung sind immun gegen die Krankheit (z.B. nach einer Impfung oder Genesung) oder sind schon selbst infiziert (können also nicht mehr angesteckt werden)?
Hängen Infektion und Krankheitsverlauf vom Alter ab? Wie ist die Altersverteilung in der Bevölkerung?
Wie wahrscheinlich ist es, dass die Krankheit bei Kontakt weitergegeben wird?
Wie wahrscheinlich ist es, dass ein Infizierter einen Gesunden trifft?
Da der Corona-Erreger neu ist, weiß man noch nicht sehr viel über diese (und noch einige andere) Bedingungen. Darum schwanken die Angaben zur Reproduktionszahl (bei der Corona-Pandemie war sie nicht so hoch wie in unserem Beispiel mit den Punkten). Aber damit die Anzahl neuer Ansteckungen zurückgeht, muss der R-Wert in jedem Fall kleiner als 1 sein. Dann werden die Menschen schneller wieder gesund, als sich die Krankheit ausbreitet.
Wie erreicht man, dass ein erkrankter Mensch möglichst wenig andere ansteckt? Leider hilft zurzeit – neben den Hygienemaßnahmen – nichts anderes als wenige Kontakte mit anderen zu haben. Denn ein Infizierter kann schon andere Menschen anstecken, wenn er noch gar nicht weiß, dass er infiziert ist. Und natürlich hoffen wir alle, dass durch Tests und Impfungen die Corona-Pandemie bald der Vergangenheit angehört. Wir wollten dir das auch nur als Beispiel nennen, damit du siehst: Mathematik kann richtig wichtig sein – eben auch wenn es darum geht, eine Krankheit zu besiegen.
