Optimierung

Es gibt viele Methoden für den Entwurf von Kontrollalgorithmen. Angefangen bei der klassischen Rückkopplungsverstärkung bis hin zu komplexeren Systemen, die invertierte Modellgleichungen oder so genannte robuste Kontrollmethoden enthalten, muss der Konstrukteur Entwurfsvariablen anpassen, damit sich das geregelte System so verhält, wie es in den Entwurfsanforderungen festgelegt ist. Je nach Steuerungsmethode ist mehr oder weniger iterative Abstimmung erforderlich, um die Einstellungen der Entwurfsvariablen mit den Entwurfsanforderungen in Einklang zu bringen. Bei komplexen Systemen mit vielen Anforderungen oder Systemen mit vielen Parametervariationen kann dies zu einer mühsamen Aufgabe werden.

Wir setzen die Designoptimierung ein, um diesen Abstimmungsprozess zu automatisieren, so dass sich das Designteam auf die Abwägung und Kompromissfindung bei potenziell widersprüchlichen Designanforderungen konzentrieren kann, anstatt sich mit Gewichtungsfunktionen oder Kontrollgesetzverstärkungen herumzuschlagen. Zu diesem Zweck hat unser Institut eine sehr geeignete Formulierung des Designproblems in Form einer Min-Max-Optimierung gefunden. Alle Designkriterien werden in rechnerischer Form wiedergegeben und auf der Grundlage intelligenter Skalierungsmethoden normalisiert, die die gewünschten Ergebnisse oder Ergebnisbereiche widerspiegeln. Diese Formulierung ist als Kreiselmeier-Steinhauser (KF)-Funktion bekannt geworden und hat sogar Anwendung in der multidisziplinären Designoptimierung (MDO) für Flugzeuge gefunden.

Wir haben ein Toolset mit der Bezeichnung Multi-Objective Parameter Synthesis (MOPS) entwickelt, mit dem das Entwicklungsteam auf bequeme Weise Kontrollgesetze oder sogar Probleme bei der Entwicklung des Gesamtsystems als eingeschränktes Min-Max-Optimierungsproblem mit potenziell Hunderten oder Tausenden von verschiedenen Kriterien formulieren kann (Algorithmen zur Lastreduzierung bei Flugzeugen sind dafür berüchtigt, da so viele Stellen der Flugzeugzelle überwacht werden müssen). Durch die Kombination verschiedener Kombinationen von Modellparametern können die Kontrollparameter für verschiedene Fälle gleichzeitig abgestimmt werden, was zu einem robusten Design führt. MOPS basiert auf Matlab oder Modelica und kann mit jeder Art von Kontrollmethode verwendet werden.

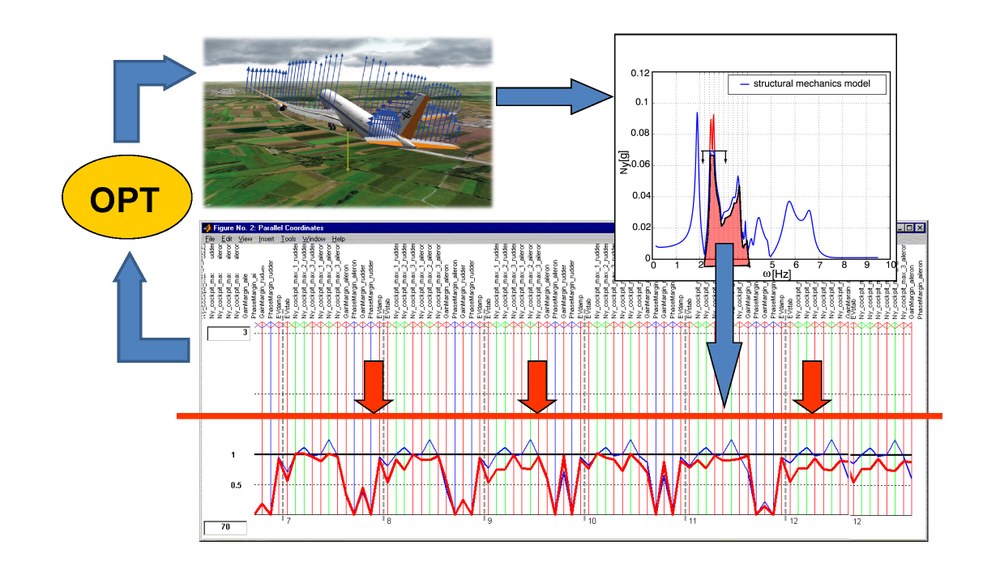
Das eigentliche Optimierungsproblem konzentriert sich auf Modellanalysen (nichtlineare Simulation, Frequenzbereichsanalysen, Mu-Analysen usw.), um alle relevanten Kriterien zu berechnen. Bei den Abstimmungsvariablen kann es sich um direkte Steuergesetzparameter wie Verstärkungen und Zeitkonstanten handeln, aber auch um Gewichtungsfunktionsvariablen, wie sie in Methoden zur Synthese robuster Steuerung verwendet werden. Das Tool bietet uns eine große Flexibilität und ermöglicht es uns, auch sehr komplexe Entwurfsprobleme zu behandeln. In der Abbildung oben sehen Sie einen Screenshot der MOPS-Benutzeroberfläche zur Visualisierung von 70 skalierten Kriterien aus 12 Szenarien. Wenn Sie auf eines der Kriterien klicken, wird die detaillierte Analyse hinter dem Kriterium visualisiert (hier: ein Frequenzgang).

Eine großartige Funktion ist auch die sogenannte Anti-Optimierung. Sobald eine gute Einstellung für die Steuergesetzparameter erreicht ist, frieren wir die Entwurfsparameter ein und verwenden die Optimierung, um stattdessen die Modellparameter einzustellen, die die Szenarien definieren. Dieses Mal versuchen wir, die Kriterien so schlecht wie möglich zu machen, so dass wir versteckte Worst-Case-Szenarien oder Kombinationen von unsicheren Modellparametern finden können. Mit diesem Wissen können wir sicherstellen, dass das System unter allen Bedingungen sicher funktioniert (dies wird als "Designverifizierung" bezeichnet), oder wir können die Abstimmung verbessern, wenn die Worst-Case-Szenarien immer noch nicht zufriedenstellend sind. Wir haben diese Methodik verwendet, um sehr effizient Kontrollalgorithmen für Hochleistungsflugzeuge, Trägerraketen usw. zu klären.