Optimisation
Design optimization is one of our key competences, as well as one of our most important tools in designing control systems, and their verification.
There are many methods for designing control algorithms. Starting from more classical feedback gains to more complex systems containing inverted model equations, or so-called robust control methods, the designer has design variables to adjust to make the closed-loop system behave as specified in design requirements. Depending on the control method, more or less iterative tuning may be required to make design variable settings and design requirements match. For complex systems with many requirements, or systems with many parameter variations, this can become a tedious task.
We use design optimization to automate this tuning process, allowing the design team to focus on balancing and compromising potentially conflicting design requirements instead of fiddling with weighting functions or control law gains. For this purpose, our institute found a very suitable formulation of the design problem in the form of min-max optimization. All design criteria are reflected in computational form and normalized based on smart scaling methods that reflect desired outcomes or outcome ranges. This formulation has become known as the Kreiselmeier-Steinhauser (KF) function and has found even application in aircraft over-all Multidisciplinary Design Optimization (MDO).
We developed a toolset, called Multi-Objective Parameter Synthesis (MOPS), that helps the design team to comfortably formulate control law, or even over-all system design problems into a constrained min-max optimization problem with potentially hundreds or thousands of different criteria (tuning loads alleviation algorithms for aircraft are notorious for this, as so many locations on the airframe have to be monitored). By combining different combinations of model parameters, control parameters can be compromise-tuned for different cases simultaneously, resulting in robust design. MOPS is Matlab or Modelica based and can be used with any type of control method.
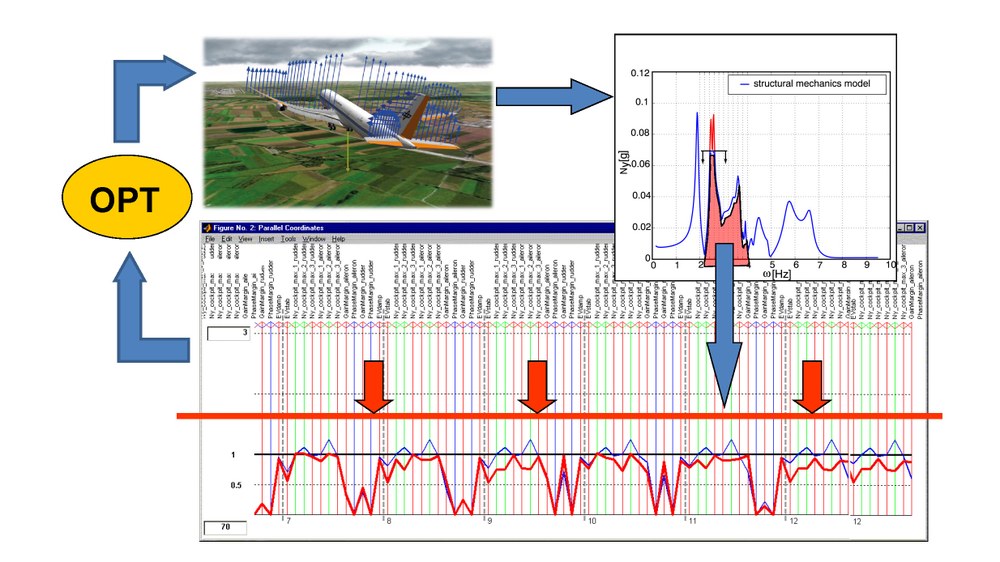
The actual optimization problem is centered around model analyses (nonlinear simulation, frequency domain analyses, mu-analysis, etc.) in order to compute all relevant criteria metrics. Tuning variables may be direct control law parameters like gains and time constants, but also weighting function variables as used in robust control synthesis methods. The tool gives us great flexibility and allows us to handle even very complex design problems. In the figure above, a screenshot of the MOPS user interface is shown to visualize 70 scaled criteria from 12 scenarios. By clicking on one of the criteria, the detailed analysis behind the criteria is visualized (here: a frequency response).
A great feature is also so-called anti-optimization. As soon as a good setting for control law parameters is reached, we freeze the design parameters and use optimization to tune model parameters instead that define the scenarios. This time, we try to make the criteria as bad as possible, allowing us to find hidden worst-case scenarios or combinations of uncertain model parameters. With this knowledge, we can make sure the system operates safely in all conditions (this is called “design verification”), or improve the tuning if the worst-cases are still not satisfactory. We used this methodology to very efficiently clear control algorithms for high performance aircraft, launchers, etc.
Of course, we also use optimization methods to find optimal trajectories for robots, cars, aircraft, and launchers, making all of these systems more energy and / or time efficient. Also, we used the same methodology to design over-all systems.
