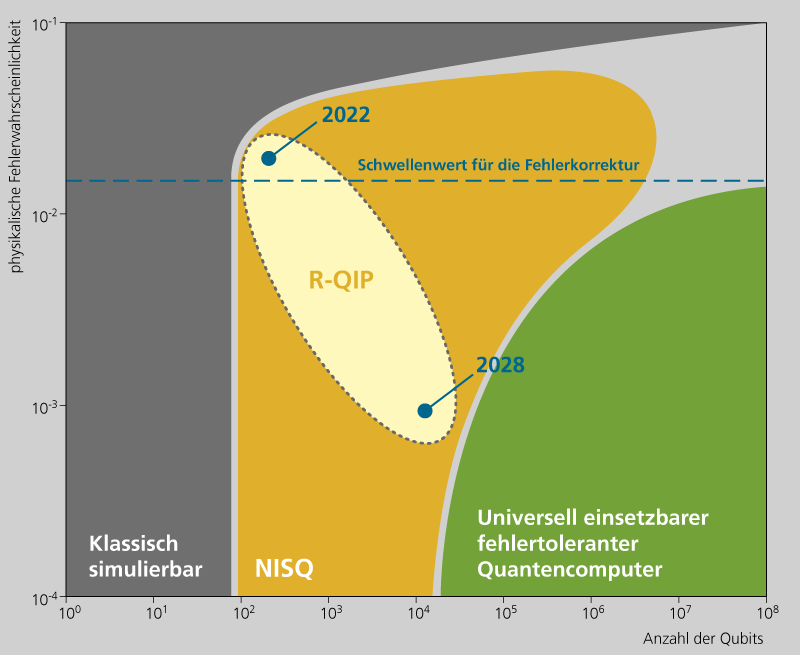
R-QIP - Reliable Quantum Information Processing
Quantum computers can solve problems that classical computers cannot. By harnessing the laws of quantum physics, enormous opportunities are opening up in nearly every application area - from traffic simulation to drug discovery to more powerful AI.
But qubits (the quantum physics counterparts to classical bits) are inherently prone to errors and information loss caused by unwanted interactions with the environment. Correcting the errors that accumulate over time in quantum computation is a key requirement for the reliable use of quantum computers.
All quantum computers realized so far operate with a computational capacity of 50 to several hundred qubits and are still highly error-prone. This is referred to as the NISQ era (Noisy Intermediate Scale Quantum). In practice, this means that the number of qubits is already large enough to solve complex problems (intermediate scale), but the results are corrupted by noise (noisy).
Thus, for quantum computation to be feasible in practice, it is necessary to introduce quantum error correction, which consists of representing logical (or information) qubits by a larger number of physical (or encoded) qubits. Thus, if some physical qubits are faulty, the remaining ones can be used to recover the logical qubits.
However, it is important that quantum error correction be as efficient as possible so that the few available qubits can be used for computational operations rather than error correction to the greatest extent possible.
The goal of R-QIP is to make quantum computation reliable and efficient in the future - using error models, simulators for quantum error correction algorithms, and new decoders for quantum error correction. Quantum codes that require fewer physical qubits to implement a (reliable) logical qubit are being investigated. Novel classes of quantum codes could significantly reduce this inefficiency, such as quantum low-density parity-check (QLDPC) codes or quantum polar codes. In practice, their performance has not yet been sufficiently investigated.
Participants in the scientific project
- DLR-Institute of Communications and und Navigation
- DLR-Institute for Software Technology
- DLR-Institute of Quantum Technologies
- DLR Space Operations and Astronaut Training
Project duration: 01/10/2022 - 28/02/2026

BMWK

