Reduzierung der Modellordnung in geometrisch nichtlinearen Analysen

Die offensichtliche, aber nicht ganz einfache Lösung besteht darin, die Linearisierungsannäherungen bei der Formulierung der Bewegungsgleichungen zu entfernen. Zu den notwendigen Anpassungen gehören: (1) Berücksichtigung eines vollständigen nichtlinearen Dehnungsmodells, (2) Berechnung der nichtlinearen Struktursteifigkeit in Abhängigkeit von den Verschiebungen. Um dies für ein FEModell zu erreichen, ist ein iterativer Ansatz mit schrittweiser Belastung erforderlich. Dies erhöht die Rechenzeiten erheblich, insbesondere bei dynamischen Belastungen. Unsere Voruntersuchungen wurden mit einem Modell reduzierter Ordnung (ROM) auf der Grundlage der Koiter-Newton Reduktionstechnik [1,2] durchgeführt. Das Besondere an dieser Methode ist, dass im Gegensatz zu vielen eigenmodenbasierten Ansätzen die Ableitungen der Eigenmoden nicht berechnet werden müssen. Vielversprechende Ergebnisse zeigen sich bei Strukturen, die der streckungsinduzierten Nichtlinearität ausgesetzt sind. Eine Reduzierung der Simulationszeit um bis zu 92 % kann für den Testfall einer flachen Platte bei guter Lösungsgenauigkeit nachgewiesen werden.

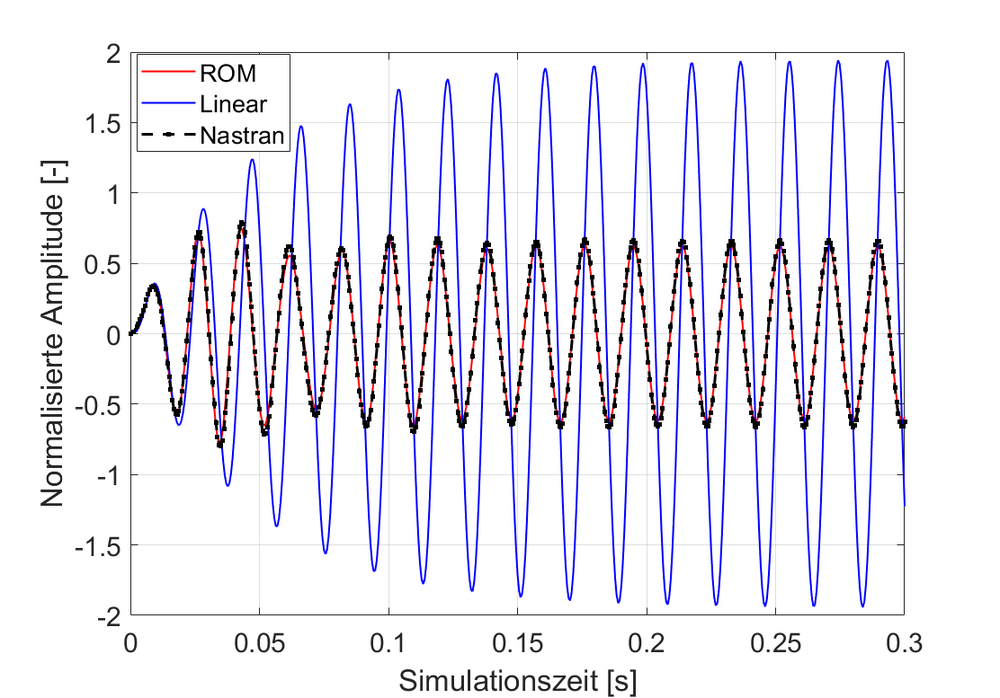
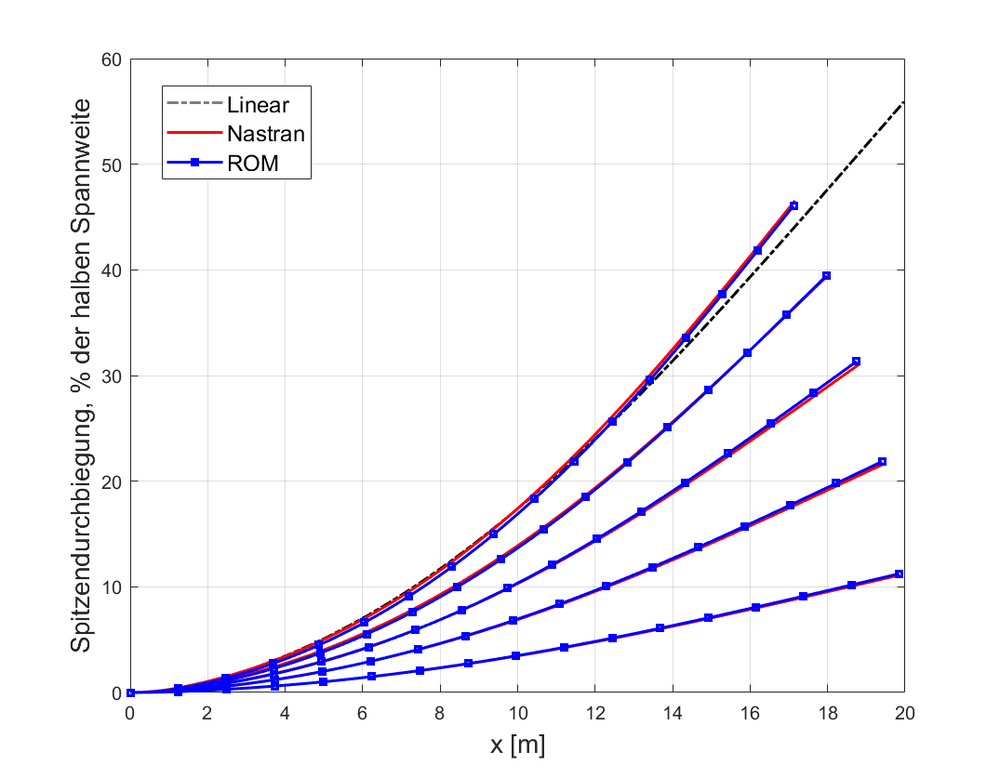
Bei der Untersuchung von eingespannten Balken wird festgestellt, dass es bis zu einer Auslenkung von etwa 15 % der Spitze (Maß für die halbe Spannweite) möglich ist, die nichtlineare Lösung mit einer Fehlergrenze von 2-3 % zu erfassen. Darüber hinaus muss das ROM aktualisiert werden, um die großen Drehungen der Geometrie zu berücksichtigen [3] und das Durchbiegungsverhalten korrekt zu ermitteln (siehe Abbildung 4). Laufende Studien zielen darauf ab, die Anwendung solcher Methoden zur Untersuchung nichtlinearer struktureller und aeroelastischer Eigenschaften von Flügelgeometrien und deren potentiellen Nutzen zu untersuchen.